Question

4 A figure was created using a trapezoid and a semicircle. Which measurement is closest to the area of the in square meters? Show Your Work A. 90 meters B,65 meters C. 100 meters D. 75 meters

Answer 1

First, we are going to calculate the area of the semicircle.

The area of a circle is given by the following expression:

`\begin{gathered} A=(\pi)/(4)\text{ }* D^2 \\ D=\text{ diameter} \\ A=(\pi)/(4)\text{ }*(8)^2 \\ A=50.26 \end{gathered}`

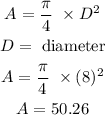
As in the figure we have a semicircle, we have to divide the value of the Area by 2,

`\begin{gathered} \text{Area of the Semicircle= }(50.26)/(2) \\ \text{Area of the Semicircle= }25.13m^2 \end{gathered}`

Now we have to calculate the area of the trapezoid,

`\begin{gathered} A=(a+b)/(2)* h \\ a=\text{ minor base} \\ b=\text{ major base} \\ h=\text{ height} \end{gathered}`
`\begin{gathered} A=(8+12)/(2)*4 \\ A=40m^2 \end{gathered}`

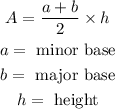
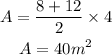
Now we add both values, area of the semicircle and area of the trapezoid,

`\begin{gathered} \text{Area semicircle + Area trapezoid = 25.13+40 } \\ \text{Area semicircle + Area trapezoid = 65.13} \end{gathered}`

Answer= 65.13 square meters