Given: An expression-
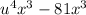
Required: To factorize the given expression.
Explanation: The difference of the square formula is-
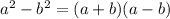
Now the given expression can be factorized as follows-
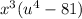
Further, we have-
![x^3[(u^2)^2-(3^2)^2]](https://img.qammunity.org/2023/formulas/mathematics/college/eu0q21vkibyymoip17ep3n8vl19paotas8.png)
Applying the difference of square formula,
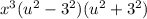
We can further factorize the expression as-
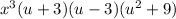
Now plotting the graph,
Let
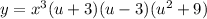
Now the graph will depend on the value of u.
The graph will be a line y=0 at u=3 and u=-3.
For u<-3, the graph is-
For -3
Finally, for u>3 we have
Final Answer: The factorized form of the expression is
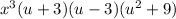
,,