Question

Factoring with repeated of the difference of square formula. Factor the answer completely. u⁴x³ – 81x³.Then graph it

Answer 1

Given: An expression-

`u^4x^3-81x^3`

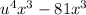
Required: To factorize the given expression.

Explanation: The difference of the square formula is-

`a^2-b^2=(a+b)(a-b)`

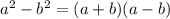
Now the given expression can be factorized as follows-

`x^3(u^4-81)`

Further, we have-

`x^3[(u^2)^2-(3^2)^2]`

Applying the difference of square formula,

`x^3(u^2-3^2)(u^2+3^2)`

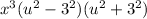
We can further factorize the expression as-

`x^3(u+3)(u-3)(u^2+9)`

Now plotting the graph,

Let

`y=x^3(u+3)(u-3)(u^2+9)`

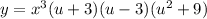
Now the graph will depend on the value of u.

The graph will be a line y=0 at u=3 and u=-3.

For u<-3, the graph is-

For -3

Finally, for u>3 we have

Final Answer: The factorized form of the expression is

`x^3(u+3)(u-3)(u^2+9)`

,,