Given the word problem, we can deduce the following information:
1. An airplane flying with the wind takes 5 hours to travel a distance of 1500 miles.
2. The return trip takes 6 hours flying against the wind.
To determine the speed of the airplane in still air and the wind speed, we follow the process as shown below. Let:
s=speed of the airplane in still air
w= speed of the wind
Next, we write the distance equation for each way:
5(s+w)=1500
6(s-w)=1500
Then, we solve for s in 5(s+w)=1500:
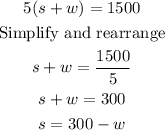
We plug in s=300-w into 6(s-w)=1500:
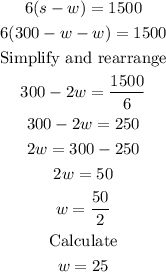
We plug in w=25 into s=300-w:
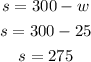
Therefore, the answers are:
The speed of the airplane in still air is 275 miles per hour.
The wind speed is 25 miles per hour.