First, we find the acceleration of the car using the following formula.
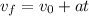
Where the final speed is zero (because the car stops), the initial speed is 86.55 km/h, and the time is 4.163 seconds. Let's replace these magnitudes and solve for a.

But, we have to transform the speed from km/h to m/s.
![\frac{86.55\operatorname{km}}{h}\cdot\frac{1000m}{1\operatorname{km}}\cdot(1h)/(3600\sec )\approx24.04((m)/(s))]()
Then, we use this transformation to find the acceleration.
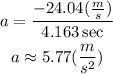
Once we have the acceleration, we can use Newton's Second Law to find the net force.
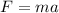
Let's replace the mass and acceleration to find F.
![\begin{gathered} F=1066\operatorname{kg}\cdot5.77((m)/(s^2)) \\ F=6150.82N \end{gathered}]()
Therefore, the net force on the car is 6150.82 Newtons.