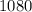Given the shaded region, you need to use the Trapezoidal Rule with:
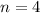
In order to approximate the area of the shaded region.
By definition, the Trapezoidal Rule is:
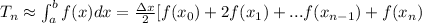
You need to find:
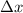
This can be found with this formula:
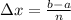
Notice in the graph that, in this case, the interval is:
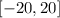
Therefore:
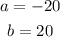
Then, by substituting values into the formula, you get:
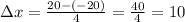
In this case, you can determine that the subintervals must begin at -20 con adding 10 until you get to 20:
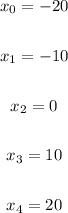
Substitute values into the Trapezoidal Rule Formula:
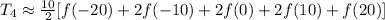
You need to use the graph to identify the y-values that correspond to each x-value. Identify the points on the curve with those coordinates:
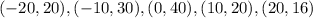
Therefore, by substituting the corresponding y-values into the formula and evaluating, you get:
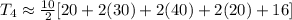
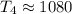
Hence, the answer is: