In the given figure of circle, radius = 12ft and the angle subtended by the arc is 60degree.
To find the area of the shaded region, subtract the area of the triangle AOB from the area of sector AOB.
Area of sector AOB :
The standard expression for the area of sector is express as;
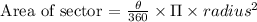
Substitute the angle = 60° and radius = 12 in the expression,
Then,
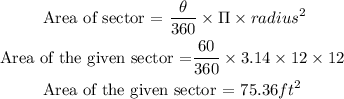
Area of the sector AOB = 75.36 ft²
Area of triangle AOB:
The standard equation for the area of triangle is;
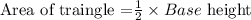
We have, the side length of the triangle, i.e. 12ft
For the base and height of the triangle,
In the given triangle AOB, draw a line perpendicular OC to the base AB, such that it bisect the angle A,
Thus, we get AC = CB and angle AOC = 30 degree, angle ACO = 90 degree
In triangle ACO,
Apply the trignometric ratio of Sin 30° for the AC of the triangle ACO,

Since, Base of triangle is AB and AC = CB
So, CB = 6ft
AB = AC + CB
AB = 6 + 6
AB = 12ft,
Thus, the base = 12ft,
Now, for the height OC,
Apply the trignometric function of cosine of angle 30°

Since, OC is the height of triangle
Height = 10.39 ft
Area of triangle AOB is ;

Now, for the area of shaded region subtract the area of triangle AOB from the sector AOB.
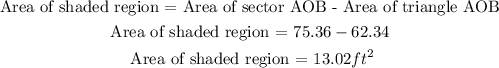
The area of shaded region is 13.02ft²
Answer : The area of shaded region is 13.02ft²