Question

1) The solutions of the quadratic equation: 3x^2+5x+10=0 Are x= _______Note: give your answer as a list of complex numbers, such as 3-4i, 5+i.

Answer 1

(1)

The given quadratic equation is,

`3x^2+5x+10=0\text{ ---(1)}`

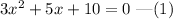
The above equation is similar to the equation given by,

`ax^2+bx+c=0\text{ ---(2)}`

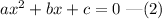
Comparing equations (1) and (2), we get a=3, b=5 and c=10.

Use discriminant method to solve equation (1).

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ =\frac{-5\pm\sqrt[]{5^2-4\cdot3\cdot10}}{2\cdot3} \\ =\frac{-5\pm\sqrt[]{25^{}-120}}{6} \\ =\frac{-5\pm\sqrt[]{-95}}{6}\text{ ---(3)} \end{gathered}`

Since

`i=\sqrt[]{-1}`

equation (3) becomes,

`\begin{gathered} x=\frac{-5\pm\sqrt[]{95}i}{6} \\ x=(-5)/(6)\pm\frac{\sqrt[]{95}}{6}i \\ x=(-5)/(6)+\frac{\sqrt[]{95}}{6}i\text{ or x=}(-5)/(6)-\frac{\sqrt[]{95}}{6}i \end{gathered}`

Therefore, the solutions of the given quadratic equation are,

`x=-(5)/(6)+\frac{\sqrt[]{95}}{6}i\text{ , x=-}(5)/(6)-\frac{\sqrt[]{95}}{6}i`