In a standard die with 6 sides, each side is numbered with a value from 1 to 6.
All sides have the same probability of being rolled, therefore each number have a probability of 1/6.
Using the formula for the expected value, we have:
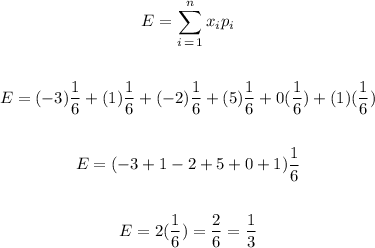
Since the expected value is positive, we can expect to win money.