To solve this question, follow the steps below.
Step 01: Find the domain.
The domain is the set of all input values, that is, all possible x values.
To find the domain, look for the restriction in the function.
Since there is only natural logarithmic for positive numbers, then:
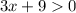
To isolate x, subtract 9 from both sides. Then, divide both sides by 3.
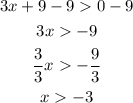
The domain is (-3, ∞), which is the same as all real numbers greater than 3.
Step 02: Find the range.
The range is the set of all possible output values. That is, the y-values that the function can achieve.
Since there are no restrictions for the y-values, the range is the set of all real numbers.
The range is (-∞, ∞), which is the same as all real numbers.
Step 03: Find the asymptote.
The vertical asymptote is a line that approaches the curve while y tends to be infinite.
We can observe that, with increasing of y value, x tends to -3 (but x will never be -3).
So, the asymptote is x = -3.
In summary:
The domain is (-3, ∞), which is the same as all real numbers greater than 3.
The range is (-∞, ∞), which is the same as all real numbers.
The asymptote is x = -3.