Question

Identify the characteristics of the logarithmic function below. If a value is a non-integer then type it as a reduced fraction: f(x)= -ln(3x+9)-7 The domain is AnswerThe range is AnswerThe vertical asymptote is x=Answer

Answer 1

To solve this question, follow the steps below.

Step 01: Find the domain.

The domain is the set of all input values, that is, all possible x values.

To find the domain, look for the restriction in the function.

Since there is only natural logarithmic for positive numbers, then:

`3x+9>0`

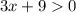
To isolate x, subtract 9 from both sides. Then, divide both sides by 3.

`\begin{gathered} 3x+9-9>0-9 \\ 3x>-9 \\ (3)/(3)x>-(9)/(3) \\ x>-3 \end{gathered}`

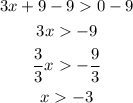
The domain is (-3, ∞), which is the same as all real numbers greater than 3.

Step 02: Find the range.

The range is the set of all possible output values. That is, the y-values that the function can achieve.

Since there are no restrictions for the y-values, the range is the set of all real numbers.

The range is (-∞, ∞), which is the same as all real numbers.

Step 03: Find the asymptote.

The vertical asymptote is a line that approaches the curve while y tends to be infinite.

We can observe that, with increasing of y value, x tends to -3 (but x will never be -3).

So, the asymptote is x = -3.

In summary:

The domain is (-3, ∞), which is the same as all real numbers greater than 3.

The range is (-∞, ∞), which is the same as all real numbers.

The asymptote is x = -3.