Question

A soft-drink bottle vendor claims that its process yields bottles with a meaninternal strength of 157 psi (pounds per square inch) and a standard deviation of 3psi and is normally distributed. As part of its vendor surveillance, a bottler strikesan agreement with the vendor that permits the bottler to sample from the vendor'sproduction to verify the vendor's claim.A) Suppose the bottler randomly selects 15 bottles to sample. What is the mean?and standard deviation?

Answer 1

Answer:

mean = 157

standard deviation = 0.77

From the given, we know that:

`\begin{gathered} \mu=157 \\ \sigma=3 \end{gathered}`

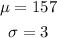
Now, since we are to select 15 bottles as samples, we now have n=15. We would then need to solve for standard deviation with the following formula:

`\sigma_x=(\sigma)/(√(n))`

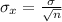
Substitute the standard deviation and n:

`\begin{gathered} \sigma_(x)=(\sigma)/(n) \\ \sigma_x=(3)/(√(15)) \\ \sigma_x=0.77 \end{gathered}`

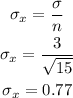
The mean would stay the same, therefore:

mean = 157

standard deviation = 0.77