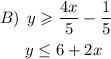
1) Since the starting point is those inequalities in the standard form, we need to perform some algebraic manipulations to get them in the slope-intercept form
2) So, let's rewrite them by adding/subtracting and dividing/multiplying terms to isolate the y-term on the left:
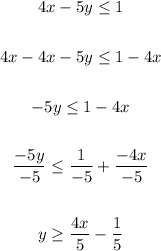
And the second inequality:
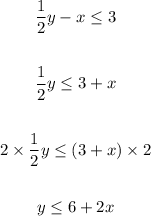
3) Examining the options, we can tell that the answer is:
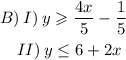
Thus, the answer is the second option (top to bottom).