Question

The graph shows the cost C in dollars al ur pounds of peanuts, a proportional relationship.

Answer 1

we are given a proportional relatrelationshipioship and the following statements:

1. 2.5 pounds of peanuts cost $1. To answer this statement we need first to find the equation of the line that models the problem. Since the relationship is proportional the equation is of the form:

`C=mx`

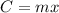
Now we replace the given point, that is: (7, 17.5), this means that when x = 7, y = 17.5. Replacing we get;

`17.5=m(7)`

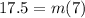
Solving for "m":

`(17.5)/(7)=m`
`2.5=m`

Replacing in the equation we get:

`C=2.5x`

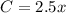
Now we replace the value of x = 2.5 pounds we get:

`\begin{gathered} C=2.5(2.5) \\ C=6.25 \end{gathered}`

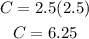
Therefore, 2.5 pounds cost $6.25. The statement is false.

2. 1 pound costs 2.5. replacing x = 1 we get:

`C=2.5(1)=2.5`

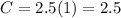
Therefore, 1 pound costs $2.5. the statement is true

3. 5 pounds of peanuts cost 12.5. Replacing x = 5

`C=2.5(5)=12.5`

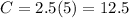
Therefore, 5 pounds cost 12.5. The statement is true:

4. 9 pounds cost 19.5. Replacing x = 9, we get

`C=2.5(9)=22.5`

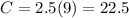
Therefore, 9 pounds cost 22.5. The statement is false.

5. The point (4,10) is on the graph. To determine this we need to replace x = 4, if we get 10, then the statement is true. Replacing x = 4 we get:

`C=2.5(4)=10`

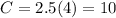
Since we got 10, the statement is true.