Question

Assume that a sample is used to population mean u. Find the margin of error M.E. that corresponds to a sample of size 10 with a mean of 26.1 and a standard deviation of 6.8 at a confidence level of 95%. Report ME accurate to one decimal place because the sample statistics are presented with this accuracy. M.E. E Answer should be obtained without any preliminary rounding. However, the critical value may be rounded to 3 decimal places

Answer 1

We have the following info given:

`\text{Mean}=10,\text{ s=6.8, n=10}`

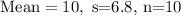
and we want to find the margin of error for the mean so we can use the following formula:

`ME=t(s)/(√(n))`

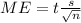
The degrees of freedom are:

`df=n-1=10-1=9`

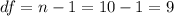
And for this case the critical value at 95% of confidence would be:

t= 2.262

And then replacing we got:

`ME=2.262\cdot(6.8)/(√(10))=4.864`

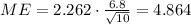
Then the margin of error for this case would be 4.864