Answer:
x=1, -1, 5, and -5.
Explanation:
Given the equation:
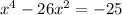
First, bring the constant term to the left-hand side of the equation:
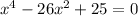
Next, rewrite the middle term using factors of 25x⁴.
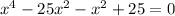
Factor the first two and last two terms:

Using the principle of difference of two squares: a²-b²=(a-b)(a+b)
![\begin{gathered} (x-1)(x+1)(x-5)(x+5)=0 \\ \implies x-1=0\text{ or }x+1=0\text{ or }x-5=0\text{ or }x+5=0 \\ \operatorname{\implies}x=1\text{ or }x=-1\text{ or }x=5\text{ or }x=-5 \end{gathered}]()
The solutions are 1, -1, 5, and -5.