Question

Two numbers product is 40 and their sum is ten what are they

Answer 1

Given that:

- The Product of two numbers is 40.

- The Sum of those numbers is 10.

You need to remember that a Product is the result of a Multiplication, and a Sum is the result of an Addition.

Let be "x" and "y" the two numbers.

Using the data given in the exercise, you can set up this System of Equations:

`\begin{cases}xy=40 \\ x+y=10\end{cases}`

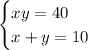
In order to solve the System of Equations, you can use the Substitution Method:

1. Solve for "y" from the second equation:

`\begin{gathered} x+y=10 \\ y=10-x \end{gathered}`

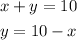
2. Substitute the new equation into the first original equation:

`\begin{gathered} xy=40 \\ x(10-x)=40 \end{gathered}`

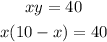
Solve for "x":

- Apply the Distributive Property on the left side of the equation:

`\begin{gathered} (x)(10)-(x)(x)=40 \\ 10x-x^2=40 \end{gathered}`

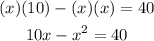
- Notice that you get a Quadratic Equation. Then, you need to rewrite it in this form:

`ax^2+bx+c=0`

Then:

`-x^2+10x-40=0`

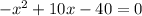
- Use the Quadratic Formula:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Knowing that:

`\begin{gathered} a=-1 \\ b=10 \\ c=-40 \end{gathered}`

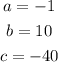
You can substitute values and simplify:

`x=\frac{-10\pm\sqrt[]{(-10)^2-4(-1)(-40)}}{2(-1)}`
`x=\frac{-10\pm\sqrt[]{-60}}{-2}`

Notice that the number inside the square root is negative. That means that you will get two Complex Solutions.

By definition:

`\sqrt[]{-1}=i`

Therefore, you need to simplify the square root of 60 and multiply it by "i":

`x=\frac{-10\pm i2\sqrt[]{15}}{-2}`

Simplifying you get: