Given that:
- The Product of two numbers is 40.
- The Sum of those numbers is 10.
You need to remember that a Product is the result of a Multiplication, and a Sum is the result of an Addition.
Let be "x" and "y" the two numbers.
Using the data given in the exercise, you can set up this System of Equations:
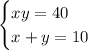
In order to solve the System of Equations, you can use the Substitution Method:
1. Solve for "y" from the second equation:
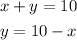
2. Substitute the new equation into the first original equation:
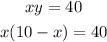
Solve for "x":
- Apply the Distributive Property on the left side of the equation:
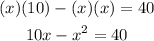
- Notice that you get a Quadratic Equation. Then, you need to rewrite it in this form:

Then:
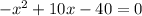
- Use the Quadratic Formula:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Knowing that:
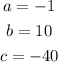
You can substitute values and simplify:
![x=\frac{-10\pm\sqrt[]{(-10)^2-4(-1)(-40)}}{2(-1)}](https://img.qammunity.org/2023/formulas/mathematics/college/tfuw8s9sne5vwk4fwwivdlr4dz0no3d5ri.png)
![x=\frac{-10\pm\sqrt[]{-60}}{-2}](https://img.qammunity.org/2023/formulas/mathematics/college/lq8ah3rj84r43ef74143c9lizeaexihao0.png)
Notice that the number inside the square root is negative. That means that you will get two Complex Solutions.
By definition:
![\sqrt[]{-1}=i](https://img.qammunity.org/2023/formulas/mathematics/high-school/6auedmvsax8nlo4hpms2kngcv15a6lmlel.png)
Therefore, you need to simplify the square root of 60 and multiply it by "i":
![x=\frac{-10\pm i2\sqrt[]{15}}{-2}](https://img.qammunity.org/2023/formulas/mathematics/college/85gza5f6l1u7k0t3xuu9nubn0xvc4gxtxo.png)
Simplifying you get:
![undefined]()