Question

How do I divide: 4x^4 - 2x^3 + x^2 - 5x + 8 by x^2 - 2x - 1, with synthetic division?

Answer 1

When we divide polynomials, remember that the rules of the signs are inverted, that means that if we have (+)(+) = - and (-)(-)=- and so on. Then, we have the following:

first we divide 4x^4 by x^2 (since it's the main term of the divisor) , we get:

`(4x^4)/(x^2)=4x^2`

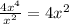
Then we write 4x^2 on our division box, and proceed like a normal long division but with the law of signs changed, to get the first substraction:

next, we do the same but now with the term 6^3, to get the following:

finally, we have the main term 17x^2, since it has the same exponent as our main term in the divisior, this is the last step to find the residue:

we have that the residue is 35x+25, then, the expression 4x^2-2x^3+x^2-5x+8 can be written as:

`4x^4-2x^3+x^2-5x+8=(x^2-2x-1)(4x^2+6x+17)+(35x+25)/(x^2-2x-1)`

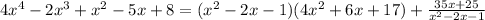
therefore, the result of dividing 4x^4-2x^3+x^2-5x+8 by x^2-2x-1 is:

`\begin{gathered} \text{ Quotient:} \\ 4x^2+6x+17\text{ } \\ \text{ Residue:} \\ 35x+25 \end{gathered}`