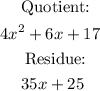When we divide polynomials, remember that the rules of the signs are inverted, that means that if we have (+)(+) = - and (-)(-)=- and so on. Then, we have the following:
first we divide 4x^4 by x^2 (since it's the main term of the divisor) , we get:
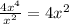
Then we write 4x^2 on our division box, and proceed like a normal long division but with the law of signs changed, to get the first substraction:
next, we do the same but now with the term 6^3, to get the following:
finally, we have the main term 17x^2, since it has the same exponent as our main term in the divisior, this is the last step to find the residue:
we have that the residue is 35x+25, then, the expression 4x^2-2x^3+x^2-5x+8 can be written as:
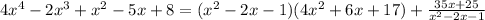
therefore, the result of dividing 4x^4-2x^3+x^2-5x+8 by x^2-2x-1 is: