Question

7)Basketball TournamentAppearancesSchoolEvansville5Ball StateSchoolAppearancesUNC Greensboro2Appalachian State2Houston Baptist1Prairie View A&M1Alabama State47SchoolAppearancesCornellRichmond9Eastern Illinois2lowa24Villanova348SouthemNortheasternCal State LA81A)B).4812 16 20 24 28 324 8 12 16 20 24 28 32C)D)+4 8 12 16 20 24 28 324 8 12 16 20 24 28 32

Answer 1

We are given the data of basketball tournament appearance of schools.

We are asked to draw a box-and-whisker plot of the data.

Recall that a box-and-whisker plot provides us the following five statistical measures.

1. Minimum value

2. Lower quartile

3. Median

4. Upper quartile

5. Maximum value

Let us calculate the above five statistical measures for the box-and-whisker plot.

First of all, arrange the data in ascending order (from least to greatest)

1, 1, 1, 2, 2, 2, 4, 5, 5, 7, 8, 8, 9

Please note that 24 and 34 seem to be outliers that's why we are not considering these two values.

As you can see from the above data,

Minimum value = 1

Maximum value = 9

The median value is located in the middle of the data set.

There are a total of 13 values.

The value at the 7th position is 4

Median = 4

The lower quartile is

`lower\: quartile=(1)/(4)(n)=(1)/(4)(13)=3.25=4th`

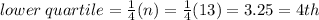
The value at the 4th position is 2

Lower quartile = 2

The upper quartile is

`lower\: quartile=(3)/(4)(n)=(3)/(4)(13)=9.75=10th`

The value at the 10th position is 7

Upper quartile = 7

Therefore, the five statistical measures are

1. Minimum value = 1

2. Lower quartile = 2

3. Median = 4

4. Upper quartile = 7

5. Maximum value = 9

From the given options, option C exactly matches with the given statistical measures.

Therefore, the correct box-and-whisker plot is option C