Given:

And θ is an angle in the standard position whose terminal side is in Quadrant IV.
We know that,
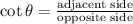
Hence, opposite side=17 and adjacent side=2
Using pythogoras theorem,
![\begin{gathered} \text{Hyp}^2=\text{Opp}^2+\text{Adj}^2 \\ \text{Hyp}^2=17^2+2^2 \\ \text{Hyp}^2=289+4 \\ \text{Hyp}^2=293 \\ \text{Hyp}=\sqrt[]{293} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/j520rn0776vzscfd65ft0idvjnjndfoisu.png)
Then the other values are,
Since θ lies in IV quadrant.
cos and sec values are positve and the others have negative values.
So,
![\begin{gathered} \sin \theta=-(opp)/(hyp) \\ =-\frac{17}{\sqrt[]{293}} \\ \cos \theta=(adj)/(hyp) \\ =\frac{2}{\sqrt[]{293}} \\ t\text{an }\theta=-\frac{\text{opp}}{\text{adj}} \\ =-(17)/(2) \\ co\sec \theta=-(hyp)/(opp) \\ =-\frac{\sqrt[]{293}}{17} \\ \sec \theta=\frac{hyp}{\text{adj}} \\ =\frac{\sqrt[]{293}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/jf5f7mvy9ywvtwrweo390crdz9rg7yw8qr.png)
Hence, the correct option is B.