The calculated value of the variable a in the expression
![\frac{2(\sqrt m)^3}{\sqrt[4]{m}} = 2m^a\\](https://img.qammunity.org/2023/formulas/mathematics/college/r3w169n3jb5utqamd83wfabss6h2a6eryb.png) is 5/4
is 5/4
How to determine the value of the expression a
From the question, we have the following parameters that can be used in our computation:
![\frac{2(\sqrt m)^3}{\sqrt[4]{m}}](https://img.qammunity.org/2023/formulas/mathematics/college/fognrjxiszsje06ng4bwuz5sgl3vy7rmtu.png)
Also, we have that this expression equals
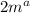
So, we have
![\frac{2(\sqrt m)^3}{\sqrt[4]{m}} = 2m^a\\](https://img.qammunity.org/2023/formulas/mathematics/college/r3w169n3jb5utqamd83wfabss6h2a6eryb.png)
Divide both sides of the equation by 2
![\frac{(\sqrt m)^3}{\sqrt[4]{m}} = m^a](https://img.qammunity.org/2023/formulas/mathematics/college/6bqf0mro3ceh49hws2cg81lu9210dxvugb.png)
This gives
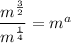
Applying the law of indices, we have
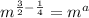
So, we have

Take the LCM and evaluate
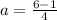
Evaluate
a = 5/4
Hence, the value of a in the expression is 5/4