We know that one root is 1-2i, and as the imaginary roots are conjugates, we obtain that the another root should be 1+2i. This means that we are able to factorize the polynomial as:
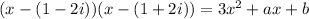
And, as such, the value of b will be the multiplication of both roots (because is the coefficient without a letter). In this case,
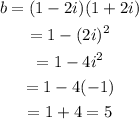
This means that the value of b must be 5.