Question

a radioactive substance of decaying so that the number of grams present after T days is given by the following function:A(t) = 450e ^ -0.04 t question 1: How many grams are left after 8 days? (round to the nearest whole gram)question 2: how long until 75 grams are left? (round to the nearest day)

Answer 1

Answer:

1) 329 grams

2) 45 days

Explanations:

The function representing the the number of grams present after t days is:

`\begin{gathered} A(t)\text{ = }450e^(-0.04t) \\ \end{gathered}`

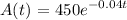
To find the number of grams left after 8 days, substitute t = 8 into the function above:

`\begin{gathered} A(8)=450e^(-0.04(8)) \\ A(8)=450e^(-0.32) \\ A(8)\text{ = }450(0.73) \\ A(8)\text{ = }328.5 \end{gathered}`

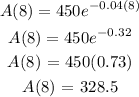
A(8) = 329 (to the nearest whole number)

329 grams are left after 8 days

2) How long until 75 grams are left

That is, A(t) = 75

To get the value of t for A(t) = 75

`\begin{gathered} 75=450e^(-0.04t) \\ (75)/(450)=\text{ }e^(-0.04t) \\ 0.167\text{ = }e^(-0.04t) \\ \ln \text{ 0.167 = -0.04t} \\ -1.79\text{ = -0.04t} \\ t\text{ = }(-1.79)/(-0.04) \\ t\text{ = }44.75 \\ t\text{ = 45} \end{gathered}`

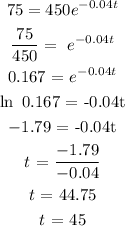
It will take 45 days for 75 grams to be left