SOLUTION:
Case: Initial value problem
An initial value problem is an ordinary differential equation together with an initial condition that specifies the value of the unknown function at a given point in the domain
To solve the initial value problem, we have a value of the derivative of y when x is known.
y'(x)= value
Given:
f(4)=2

The resulting equation will be:
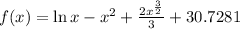
Final answer:
![f(x)=\operatorname{\ln}x-x^2+\frac{2x^{(3)/(2)}}{3}+30.7281]()