Lets calculate the wavelength of the sound in water. But before we do that, we must transform the unit of the speed to m/s. We get:
5220 / 3,6 = 1450 m/s
So
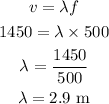
The wave of sound does not change the frequency as it goes through different mediums. So f = 500 Hz. The speed of sound in air is 340 m/s. Then we can say that:
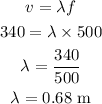
We can see how many times more wavelengths occur in air by calculating the ratio:
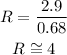
So wavelengths in air occur approximately 4 times more than in water.