We are given that $10 000 is continuously compounded, and we are asked to determine the rate of change that will produce $25 000 in ten years. To do that we will use the following formula:
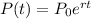
Where:
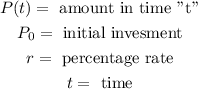
Now, we will solve for the value of "r". First, we will divide both sides by P0:
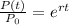
Now, we take the natural logarithm to both sides:
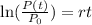
Now, we divide both sides by the time "t":
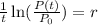
Now, we plug in the values:
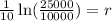
Now, we solve the operations:
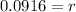
This is the interest rate in decimal form. To get the percentage we multiply by 100, and we get:
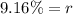
Therefore, the interest rate is 9.16%