Question

An investment of $10,000 is compounded continuously. What annual percentage rate will produce a balance of $25,000 in ten years?

Answer 1

We are given that $10 000 is continuously compounded, and we are asked to determine the rate of change that will produce $25 000 in ten years. To do that we will use the following formula:

`P(t)=P_0e^(rt)`

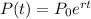
Where:

`\begin{gathered} P(t)=\text{ amount in time ''t''} \\ P_0=\text{ initial invesment} \\ r=\text{ percentage rate} \\ t=\text{ time} \end{gathered}`

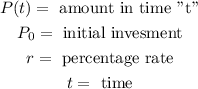
Now, we will solve for the value of "r". First, we will divide both sides by P0:

`(P(t))/(P_0)=e^(rt)`

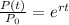
Now, we take the natural logarithm to both sides:

`\ln((P(t))/(P_0))=rt`

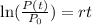
Now, we divide both sides by the time "t":

`(1)/(t)\ln((P(t))/(P_0))=r`

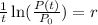
Now, we plug in the values:

`(1)/(10)\ln((25000)/(10000))=r`

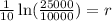
Now, we solve the operations:

`0.0916=r`

This is the interest rate in decimal form. To get the percentage we multiply by 100, and we get:

`9.16\%=r`

Therefore, the interest rate is 9.16%