Question

I just need help with plotting the points on the graph

Answer 1

The graph of the parabola is shown below:

To find the vertex we need to complete the squares of the equation, let's do this:

`\begin{gathered} y=15x^2-x-6 \\ y=15(x^2-(x)/(15))-6 \\ y=15(x^2-(x)/(15)+(-(1)/(30))^2)-6-15((1)/(30))^2 \\ y=15(x-(1)/(30))^2-6-(1)/(60) \\ y=15(x-(1)/(30))^2-(361)/(60) \end{gathered}`

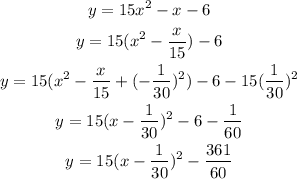
Therefore, the vertex of the parabola is at (1/30,-361/60) which can be express as (0.033,-6.017).

The y intercept happens when x=0, plugging this in the equation we have:

`\begin{gathered} y=15(0^2)-0-6 \\ y=-6 \end{gathered}`

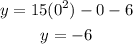
then, the y-intercept have coordinates (0,6).

Finally, the x-intercepts happens when y=0, plugging this in the equation and solving for x we have:

`\begin{gathered} 15x^2-x-6=0 \\ \text{ Using the quadratic formula we have:} \\ x=(-(-1)\pm√((-1)^2-(4)(15)(-6)))/(2(15)) \\ x=(1\pm√(361))/(30) \\ x=(1\pm19)/(30) \\ \text{ then} \\ x=(1+19)/(30)=(20)/(30)=(2)/(3) \\ \text{ or} \\ x=(1-19)/(30)=-(18)/(30)=-(3)/(5) \end{gathered}`

Therefore, the x-intercepts of the parabola are (2/3,0) and (-3/5,0) that can be written as (0.667,0) and (-0.6,0). Finally the parabola opens up, as we see on the graph.