Question

Graph the following system of equations and find the y-coordinate of the solution.

Answer 1

From the problem, we have :

`\begin{gathered} 3x+3y=3 \\ y=-(1)/(2)x+2 \end{gathered}`

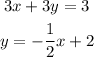
Find the x and y intercepts of the lines to graph the following equations.

For 3x + 3y = 3

x-intercept :

`\begin{gathered} 3x+\cancel{3y}=3 \\ x=(3)/(3)=1 \end{gathered}`

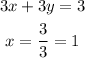
y-intercept :

`\begin{gathered} \cancel{3x}+3y=3 \\ y=(3)/(3)=1 \end{gathered}`

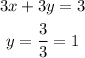
The points are (1, 0) and (0, 1)

For y = -1/2 x + 2

y-intercept :

`\begin{gathered} y=\cancel{-(1)/(2)x}+2 \\ y=2 \end{gathered}`

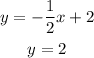
x-intercept :

`\begin{gathered} \cancel{y}=-(1)/(2)x+2 \\ (1)/(2)x=2 \\ x=4 \end{gathered}`

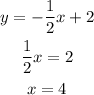
The points are (0, 2) and (4, 0)

Plot the points :

The solution is the intersection between two lines.

The intersection is at (-2, 3)

The y coordinate is 3

The answer is B. y = 3