From the problem, we have :
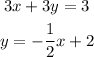
Find the x and y intercepts of the lines to graph the following equations.
For 3x + 3y = 3
x-intercept :
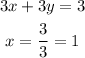
y-intercept :
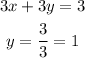
The points are (1, 0) and (0, 1)
For y = -1/2 x + 2
y-intercept :
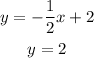
x-intercept :
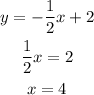
The points are (0, 2) and (4, 0)
Plot the points :
The solution is the intersection between two lines.
The intersection is at (-2, 3)
The y coordinate is 3
The answer is B. y = 3