We are given that the function of demand is given as:
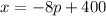
Where:
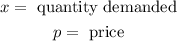
The function of revenue is given by:
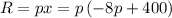
Applying the distributive law we get:
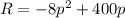
We get an equation of the form:
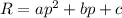
This is a quadratic equation and its graph is a parabola.
If the value of "a" is negative this means that the parabola opens downwards, therefore, the possible answers are A or D.
We notice that A is the graph of p vs R. Since our equation is a function of "p" we need R vs P, therefore, the right answer must be D.