Question

Help me please.The price p(in dollars) and the quantity x sold of a certain product satisfy the deman equation x=-8p+400. Answer the following questions(f) choose the graph (g) what price should the company charge to earn at least 4200 in revenue?The company should charge a price between a minimum of ____$ and a max of _____$.

Answer 1

We are given that the function of demand is given as:

`x=-8p+400`

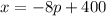
Where:

`\begin{gathered} x=\text{ quantity demanded} \\ p=\text{ price} \end{gathered}`

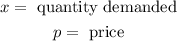
The function of revenue is given by:

`R=px=p\left(-8p+400\right)`

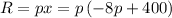
Applying the distributive law we get:

`R=-8p^2+400p`

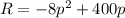
We get an equation of the form:

`R=ap^2+bp+c`

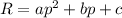
This is a quadratic equation and its graph is a parabola.

If the value of "a" is negative this means that the parabola opens downwards, therefore, the possible answers are A or D.

We notice that A is the graph of p vs R. Since our equation is a function of "p" we need R vs P, therefore, the right answer must be D.