ANSWER
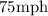
Step-by-step explanation
Let Dani's speed be x.
Ray drives 15 mph faster than Dani does. This means that Ray's speed is:
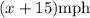
Ray can drive 100 miles in the same amount of time that Dani drives 80 miles.
We have to calculate Dani's speed in driving 80 miles and ray's speed in driving 100 miles.
Let t be the time for both, since their times are equal.
Therefore, for Dani:

For Ray:

Equate the values of t:

Therefore, Ray's driving speed is:
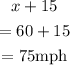
Ray's driving speed is 75 mph.