Answer:
4.2 inches
Step-by-step explanation:
First, we need to calculate the length of AB. It can be calculated using the trigonometric function tangent because
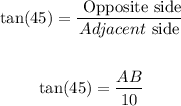
Because 45 = 30 + 15. Now, we can solve for AB as follows
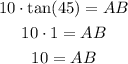
Using the same trigonometric function, we can calculate the length of DB, so

Now, the length of AD is equal to
AD = AB - BD
AD = 10 - 5.77
AD = 4.23
Therefore, the answer is 4.2 inches