Question

Consider the function h(x) = x^3 + 2x^2 - 15x.What are the zeros of h(x)?Smallest zero:Middle zero:Largest zero:

Answer 1

We are given

`h(x)=x^3+2x^2-15x`

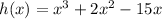
We want to find the zeros of h(x)

Solution

Finding the zeros of h(x) means that we should equate h(x) to zero and solve

`\begin{gathered} i\mathrm{}e \\ h(x)=0 \end{gathered}`

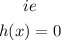
We now solve for h(x) = 0

`\begin{gathered} h(x)=0 \\ h(x)=x^3+2x^2-15x=0 \\ x^3+2x^2-15x=0 \\ x(x^2+2x-15)=0 \end{gathered}`

We also factorize the quadratic as well

`\begin{gathered} x^2+2x-15 \\ x^2+5x-3x-15 \\ (x^2+5x)-(3x+15) \\ x(x+5)-3(x+5) \\ (x+5)(x-3) \end{gathered}`

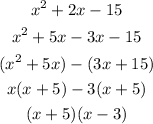
We come back to

`\begin{gathered} x(x^2+2x-15)=0 \\ x(x+5)(x-3)=0 \\ \text{therefore,} \\ x=0 \\ or \\ x+5=0 \\ x=-5 \\ or \\ x-3=0 \\ x=3 \end{gathered}`

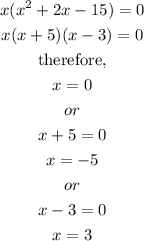
Thus,

The zeros are x = 0, x = -5 and x = 3

Smallest zero = -5

Middle zero = 0

Largest zero = 3