In this problem we are given that a person who wants to go to a party would like to bring 3 different bags of chips; and also, that he/she has 13 varieties.
As she has differents options to choose, we see that this one is a problem of permutations or combinations. But the order of the chips the person brings does not matter, and so, we have to find a combination. We remember then that the equation for finding a combination of n objects and k possibilites is given by the following binomial coefficient
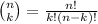
Where the symbol ! represents factorial (the product of the number to the number). For example,
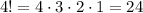
Now, in our exercise, we have that the person has 13 varieties and has to choose 3 of them. We have to calculate then:
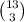
For doing so, we will start by replacing the values on the formula:

And cancelling the equal terms, we obtain:

This means that the person would be able to do 286 different selections.