Question

Find the to numbers whose product is 24 and whose sum is 14

Answer 1

Let x represent one of the unknown numbers and y represent the other.

The product of both numbers is 24: xy=24

The sum of both numbers is 14: x+y=24

With this we determined a 2 unknown equation system.

Now write one of the equation is terms of one of the variables, for example write the second equation for x:

`\begin{gathered} x+y=14 \\ x=14-y \end{gathered}`

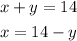
Replace it in the first one

`\begin{gathered} xy=24 \\ (14-y)y=24 \end{gathered}`

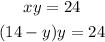
Solve the parentheses applying the distributive propperty of multiplication:

`14y-y^2=24`

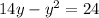
Set the equal to zero:

`-y^2+14y-24`

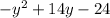
Using the quadratic formula solve for the possible values of y:

`y=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

For the expression determined a=-1, b=14 and c=-24, replace in the formula and calculate

`\begin{gathered} y=\frac{-14\pm\sqrt[]{14^2-4(-1)(-24)}}{2(-1)} \\ y=\frac{-14\pm\sqrt[]{100}}{-2} \\ y=(-14\pm10)/(-2) \end{gathered}`

Now solve for the two possible values of y

Positive:

`\begin{gathered} y=(-14+10)/(-2) \\ y=2 \end{gathered}`

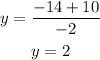
Negative:

`\begin{gathered} y=(-14-10)/(-2) \\ y=12 \end{gathered}`

y has two possible outcomes 2 and 12, for both values you have to calculate the value of x using either equation:

For y=2

`\begin{gathered} xy=24 \\ x=(24)/(y) \\ x=(24)/(2) \\ x=12 \end{gathered}`

For y=12

`\begin{gathered} x+y=14 \\ x=14-y \\ x=14-12 \\ x=2 \end{gathered}`

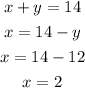
The numbers whose product is 24 and sum is 14 are 2 and 12