Question

The velocity function, in meters per minute, of a particle moving along a straight line isv(t)=5t−2,where t is time in minutes.1. Find the displacement of the particle from t=2 minutes to t=5 minutes?meters Tries 0/992. Find the time t when the displacement is zero after the particle starts moving?minutes

Answer 1

Part A. We are given that the velocity function of a particle is given by:

`v(t)=5t-2`

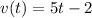
We are asked to determine the displacement. To do that we need to determine the formula for the distance. Let's remember that the distance is given by:

`s(t)=\int v(t)dt`

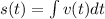
Now, we substitute the formula for the velocity:

`s(t)=\int(5t-2)dt`

Now, we distribute the integral:

`s(t)=\int5tdt-\int2dt`

Now, we use the following formula for integration:

`\int x^ndx=(x^(n+1))/(n+1)+c`

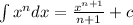
Applying the rule we get:

`s(t)=(5t^2)/(2)-2t+c`

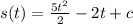
Now, to determine the displacement we need to determine the difference between the positions, like this:

`d=s(5)-s(2)`

Now, we substitute the values in the formula for the position:

`\begin{gathered} s(5)=(5(5)^2)/(2)-2(5)+c=(105)/(2)+c \\ \\ s(2)=(5(2^2))/(2)-2(2)+c=6+c \end{gathered}`

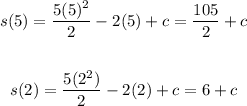
Now, we substitute in the formula for the displacement:

`d=(105)/(2)+c-6-c`

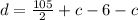
Solving the operations:

`d=(93)/(2)=46.5`

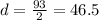
Therefore, the displacement is 46.5 minutes

Part B. The displacement of the particle between an initial time "t = 0" and a final time "t" is:

`d=s(t)-s(0)`

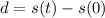
Substituting we get:

`d=(5t^2)/(2)-2t+c-(5(0)^2)/(2)+2(0)-c`

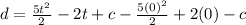
Solving the operations:

`d=(5t^2)/(2)-2t`

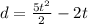
Now, we set the displacement to zero:

`(5t^2)/(2)-2t=0`

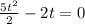
Now, we take "t" as a common factor:

`t((5t)/(2)-2)=0`

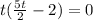
Since we want the value of time that is different from zero we set the second factor to zero:

`(5t)/(2)-2=0`

Now, we add 2 to both sides:

`(5t)/(2)=2`

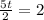
Now, we multiply both sides by 2:

`5t=4`

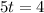
Now, we divide both sides by 5:

`t=(4)/(5)=0.8`

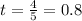
Therefore, the time is 0.8 minutes.