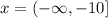Question

consider the functions f(x)=x+9 and g(x)= √-x-1. Determine each of the following.(f°g)(x)=Give the domain of (f°g)(x).____(g°f)(x)=Give the domain of (g°f)(x).____

Answer 1

First:

`(f\circ g)(x)=\sqrt[]{-x-1}+9`

The domain of this function is when the term under the root is positive or 0 because there is no root for a negative number in the real numbers, this only happens when:

`-x-1\ge0\Rightarrow-x\ge1\Rightarrow x\leq-1`

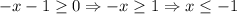
Then, the domain is when x is:

`x=(-\infty,-1\rbrack`

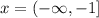
Then, for the second part:

`(g\circ f)(x)=\sqrt[]{-(x+9)-1}=\sqrt[]{-x-10}`

The domain for this function is only when the term under the root is positive or 0, so:

`-x-10\ge0\Rightarrow-x\ge10\Rightarrow x\leq-10`

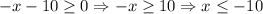
Then, the domain is:

`x=(-\infty,-10\rbrack`