Answer:
y+3=-4(x-5)
Step-by-step explanation:
Part A
Given the line:
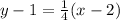
We want to find the equation of a perpendicular line that passes through the point (5,-3),
First, determine the slope of the perpendicular line.
Comparing the given line with the slope-point form:
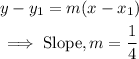
By definition, two lines are perpendicular if the product of their slopes is -1.
Let the slope of the perpendicular line = n
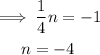
Thus, using a slope of -4 and a point (5,-3), we find the equation of the line.
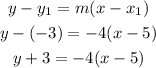
The equation of the perpendicular line in the slope-point form is:
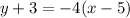
Part B
In order to graph the line, first, find two points on the line.
When x=0
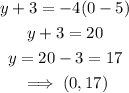
When y=1
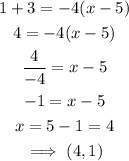
Join the points (0,17) and (4,1) as shown in the graph below: