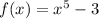Step 1. To find which function has an inverse function, we will use the horizontal line test.
Horizontal line test: If you draw a horizontal line and it touches the graph at two or more points, the function is not a one-to-one function, and therefore it does not have an inverse function.
For example:
Let's analyze the functions given in the options until we found the one that has an inverse function.
Step 2. The first function we have is:
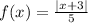
The graph of this function looks as follows:
We can draw a horizontal line and it will touch the graph at two points:
Therefore, the function is not a one-to-one function and it does not have an inverse function.
Step 3. The next function is:
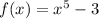
The graph looks as follows:
In this case, the horizontal lines will only touch the graph at one point:
Since it is a one-to-one function, it will have an inverse function.
Answer: