When we have a right triangle, the hypotenuse c is always greater than the sides a and b.
Remember that the hypotenuse is the side opposed to the right angle.
Using the Pythagorean Theorem, it is known that for a right triangle of sides a, b, and c with hypotenuse c, the following condition is satisfied:

Check each option in order to know if those are the sides of a right triangle:
A) 12, 16, 20
Since the longest side is 20, if those were the sides of a right triangle, 20 would be the hypotenuse.
Check if the condition is satisfied. On the left hand side of the equation, we have:
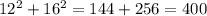
On the right hand side of the equation:
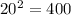
Since 12^2+16^2=20^2, then those are the lenghts of the sides of a right triangle.
B) 4.5, 6, 7.5
Since the longest side is 7.5, check the condition:
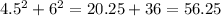
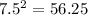
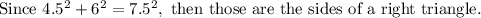
C) 5, 12, 13
Since 13 is the longest side:
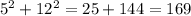


D) 6, 12, 14
Since 14 is the longest side:
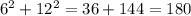

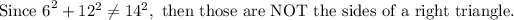
E) 5, 7, 10
Since 10 is the longest side:

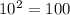
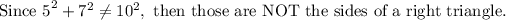
Therefore, the options which could be the side lenghts of a right triangle are A, B, and C.