Question

A 50 foot ladder is set against the side of a house so that it reaches up 48 feet.

Answer 1

45.8

After moving the base 6ft farther, the ladder will reach 45.8ft far up the side of the house.

Explanation:

h2+(14+6)2=502h2+202=502h2=

502−202h2=(50+20)(50−20)h

2=70⋅30h=2100h=1021h

=45.8257569496…h≈

Answer 2

The ladder and the house wall form a right triangle given by the scheme below

Where x represents the distance between the base of the ladder and the house wall.

After moving the ladder 6 ft farther, a new triangle is generated with the following measures

where h represents how far up the ladder is on the house wall.

Using the Pythagorean theorem on both triangles, which states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides“, we get the following system.

`\begin{gathered} 48^2+x^2=50^2 \\ h^2+(x+6)^2=50^2 \end{gathered}`

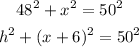
Solving the first equation for x, we have

`\begin{gathered} 48^2+x^2=50^2 \\ x^2=50^2-48^2 \\ x^2=(50+48)(50-48) \\ x^2=98\cdot2 \\ x^2=196 \\ x=\sqrt[]{196} \\ x=14 \end{gathered}`

Using this x value on the second equation, we can determinate the height of the second triangle.

`\begin{gathered} h^2+(14+6)^2=50^2 \\ h^2+20^2=50^2 \\ h^2=50^2-20^2 \\ h^2=(50+20)(50-20) \\ h^2=70\cdot30 \\ h=\sqrt[]{2100} \\ h=10\sqrt[]{21} \\ h=45.8257569496\ldots \\ h\approx45.8 \end{gathered}`

After moving the base 6ft farther, the ladder will reach 45.8ft far up the side of the house.