We have two triangle UTS, and WXV, they are simillar because all of their angles are equal. This is demonstrated by the fact the angle U and W are:
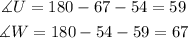
This means that every corresponding sides of the triangles are related by the same constant. We can use this fact to calculate VW, as shown below:
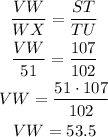
The side VW has a length of 53.5