First, plot the points for a better visual intuition:
The points A and B are vertices of the parallelogram, and O is the point where the diagonals meet.
Let C(x_c,y_c) be the vertex opposite to A, as well as D(x_d,y_d) the vertex opposite to B.
The point O, were the diagonals meet, is the midpoint of both diagonals. Use the midpoint formula to write down equations that will determine the values of the coordinates of C and D:
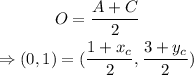
Find x_c and y_c:
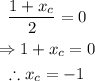
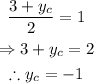
Then, the coordinates of the point C are (-1,-1).
Since O is also the midpoint of B and D, we can find via a similar process that the coordinates of D are (-2,2). The full picture of the parallelogram is:
By calculating the length of the sides, we can notice that this parallelogram is in fact a square.
Therefore, the locations of the remaining vertices are at (-2,2) and (-1,-1). The most specific classification of this parallelogram is a square.