The given equation is
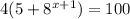
Divide both sides by 4
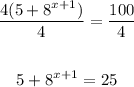
Subtract 5 from each side
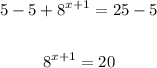
Insert log on both sides
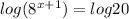
Use the rule of the power
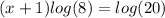
Divide both sides by log(8)

Subtract 1 from both sides
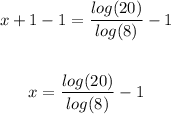
a)
The exact solution is
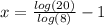
b)
By using the calculator the solution is
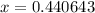
The answer is x = 0.440643 to the nearest 6 decimal place