Question

4(5 + 8x + 1) = 100(a) Find the exact solution of the exponential equation in terms of logarithms.x = (b) Use a calculator to find an approximation to the solution rounded to six decimal places.x =

Answer 1

The given equation is

`4(5+8^(x+1))=100`

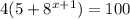
Divide both sides by 4

`\begin{gathered} (4(5+8^(x+1)))/(4)=(100)/(4) \\ \\ 5+8^(x+1)=25 \end{gathered}`

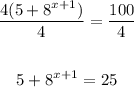
Subtract 5 from each side

`\begin{gathered} 5-5+8^(x+1)=25-5 \\ \\ 8^(x+1)=20 \end{gathered}`

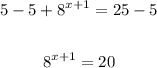
Insert log on both sides

`log(8^(x+1))=log20`

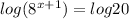
Use the rule of the power

`(x+1)log(8)=log(20)`

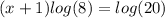
Divide both sides by log(8)

`\begin{gathered} ((x+1)log(8))/(log(8))=(log(20))/(log(8)) \\ \\ x+1=(log(20))/(log(8)) \end{gathered}`

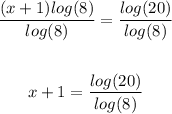
Subtract 1 from both sides

`\begin{gathered} x+1-1=(log(20))/(log(8))-1 \\ \\ x=(log(20))/(log(8))-1 \end{gathered}`

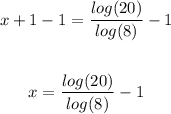
a)

The exact solution is

`x=(log(20))/(log(8))-1`

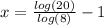
b)

By using the calculator the solution is

`x=0.440643`

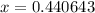
The answer is x = 0.440643 to the nearest 6 decimal place