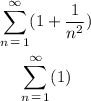Question

Provide an example of two series , and b that both diverge, but (a -b.) converges.

Answer 1

Let the sequence a_n be equal to:

`a_n=1+(1)/(n^2)`

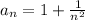
And the sequence b_n be equal to:

`b_n=1`

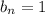
Notice that both series diverge:

`\begin{gathered} \sum ^(\infty)_(n\mathop=1)a_n=\sum ^(\infty)_(n\mathop=1)(1+(1)/(n^2))\rightarrow\infty \\ \sum ^(\infty)_(n\mathop=1)b_n=\sum ^(\infty)_(n\mathop=1)(1)\rightarrow\infty \end{gathered}`

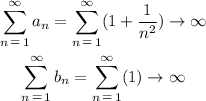
Nevertheless, notice that the sequence a_n-b_n is given by:

`\begin{gathered} a_n-b_n=(1+(1)/(n^2))-1 \\ =(1)/(n^2) \end{gathered}`

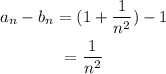
Then:

`\sum ^(\infty)_(n\mathop=1)(a_n-b_n)=\sum ^(\infty)_(n\mathop=1)(1)/(n^2)`

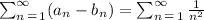
It is a famous result that:

`\sum ^(\infty)_(n\mathop=1)(1)/(n^2)=(\pi^2)/(6)`

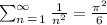
Then we found two divergent series so that each series diverge and the series of the difference a_n-b_n converge. The series are:

`\begin{gathered} \sum ^(\infty)_(n\mathop=1)(1+(1)/(n^2)) \\ \sum ^(\infty)_(n\mathop=1)(1) \end{gathered}`